자료구조의 시간복잡도

빅오(O(n))표기법은 실제 러닝타임을 데이터나 사용자의 증가율에 따라 알고리즘의 성능을 예측하는 것으로 알고리즘이 시간과 공간을 어마나 차지하는지를 수학적으로 표현한것이다.

왜 사용하는가?

해당 알고리즘이 얼마나 효율적으로 작동하는지를 쉽게 알아볼수 있다

 

배열이 주어졌을때 두수의 차를 구하는 시간 복잡도 O(n^2)

n*n = n^2

n제곱의 연산을 구해야한다.

문제가 커지면 커질수록 매우 느려진다 10*10 = 100

	2	5	6	...	16
2	n/a	3	4	...	15
5	3	n/a	1	...	11
6	4	1	n/a	...	10
...	...	...	...	...	...
16	14	11	10	...	n/a

 

가장 큰수와 가장 작은수

2	5	6	...	16
is smallest	Y	N	...	N
ls largest	Y	Y	...	Y

 

16이 가장 큰 수라 했을때 n번의 연산을 한것이다.

 

연산 횟수를 카운팅 할때 3가지 경우가 있다.

1. 최선의 경우 Best Case
2. 최악의 경우 Worst Case
3. 평균적인 경우 Average Case

평균적인 경우 가장 이상적으로 보이겠지만 알고리즘이 복잡해 질수록 평균적인 경우는 구하기가 매우 어려워 진다. 그러므로 최악의 경우로 알고리즘의 성능을 파악한다.

 

 

O(1) Constant

• 일력되는 데이터양과 상관없이 일정한 실행 시간을 갖는다.
• 알고리즘의 문제를 해결하는데 오직 한 단계만 거친다.
• 입력데이타의 크기에 상관없이 일정한 시간이 걸리는 알고리즘을 말한다.

 

O(longN) Logarithmic

• binary search
• 데이터의 양이 많아져도, 시간이 조금 늘어난다.
• 시간에 비례하여, 탐색 가능한 데이터양이 2의 n승이 된다.

O(N) Linear

• 데이터 양에 따라 시간이  비례한다.
• for linear search 를 통한 탐색을 생각하면 된다.
• 입력데이타의 크기에 비례해서 처리시간이 걸리는 알고리즘을 표현할때 사용한다.

O(n^2)

• 이중 반복문같은 경우의 시간 복잡도
• 처음에는 조금씩 상승하다가 나중에는 하나 추가해도 엄청나게 증가한다.

array의 시간 복잡도

Lookup: 인덱스의 위치를 알고 그 값을 반환할때 O(1) 의 시간 복잡도를 갖는다

Assign: 배열안에 값을 다른 값으로 바꿀때 O(1) 의 시간 복잡도를 갖는다

Insert: 배열안에 값을 추가할때 , 운이 좋아서 끝에 될 경우를 제외하고 . 최악의 경우 데이타 개수 만큼 옮겨야해서 O(n) 의 시간 복잡도를 갖는다

Remove : 지우면 다시 빈 공간을 채워줘야 하므로O(n) 의 시간 복잡도를 갖는다

Find(Value): 특정 포지션을 모르면 0번째 인덱스 부터 확인해줘야 하므로 O(n) 의 시간 복잡도를 갖는다

 

Linked list

Lookup,Assign, Find:헤드부터 하나하나 가야하기 때문에 O(n) 의 시간복잡도를 갖는다

insert: 다음 노드를 찾아갈 링크만 바꿔주면 되기 때문에 O(1) 의 시간복잡도를 갖는다

Remove: 위치를 알고 있다면 첫번째를 다음번째로 바꾸고 루트만 바꿔주면 되지만 단방향은 전의 값을 알지 못하기때문에

head:  O(1) , middle: O(n) 의 시간복잡도를 갖는다.

doubly-Liked List: 해당 값의 전값을 알수 있기 때문에 remove에 경우 O(1)을 갖는다.

 

 

 

 

Tree

Lookup,Assign, Find,remove,Insert: root부터 하나하나 가야하기 때문에 O(n) 의 시간복잡도를 갖는다

Find: 최악의 경우 모든걸 다 찾아야 하기때문에 O(n)

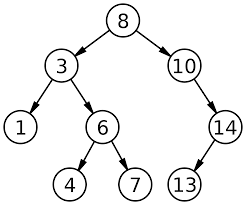
Binary Search Tree

왼쪽은 부모보다 작은거 오른쪽은 부모보다 큰거를 찾기 때문에 O(log n)을 갖게된다.

Lookup,Assign, Find,remove,Insert: O(log n)

밸런스가 안좋은 경우 한쪽으로 몰리게 되면 O(n)을 갖을수도 있다.

방지 방법: 밸런스가 무너 질 때 마다 트리를 비틀어 값을 넣어주게 된다. O(log n)

 

 

hash table 시간복잡도

검색할 값을 입력하면 해시 펑션을 거쳐 바로 해당 인덱스로 갈수 있기 때문에 O(1)의 시간복잡도를 갖는다.

그러나 충돌이나 값이 많이 들어올경우 O(n)의 시간복잡도를 갖을수 있기 때문에 충돌을 잘 해결해 나가야 한다.